P
Télécharger le PDF du cours
Soutenez-nous sur Patreon pour télécharger
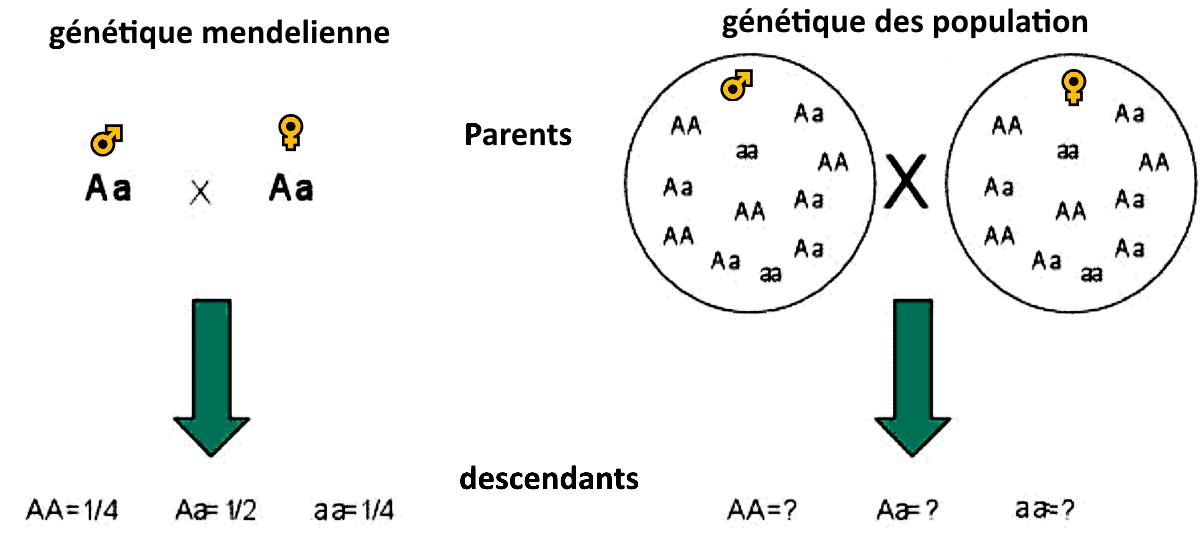
Introduction
La génétique des populations est la branche de la génétique qui s’intéresse à l'étude de la variabilité génétique présente dans les populations, elle vise à : mesurer la variabilité génétique, et suivre la transmission de cette variabilité d’une génération à l’autre.
- Comment calculer la variabilité génétique ?
- Quels sont les facteurs influençant la variabilité génétique des populations ?
I – Notion de la population et du pool génétique

1 – Notion de la population
La population est un ensemble d’individus appartenant à la même espèce vivant dans le même espace géographique et pouvant se croiser entre eux.
La population se caractérise donc par des critères spatiaux, temporels et génétiques. Et, elle constitue une structure dynamique qui évolue par :
- L’entrée de nouveaux individus : naissance, migration vers la population.
- La perte d’individus : mortalité, migration en dehors de la population.
2 – Notion du pool génétique
Une population est caractérisée par une composition génétique formée de l’ensemble des génotypes de ses individus. Il s’agit d’un génome collectif (global) appelé pool génique : c’est l’ensemble des allèles qui se trouvent sur les locus des gènes des chromosomes de tous les individus de la population.
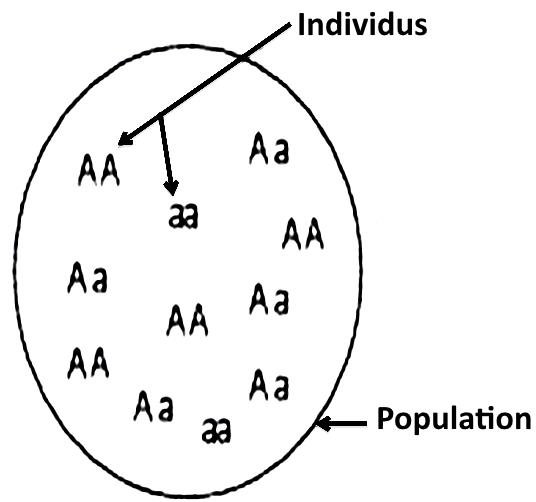
Exemple : La figure suivante présente un schéma du pool génétique, d’un locus d’un gène représenté par deux allèles A et a, dans une population constituée de 11 individus.
Cette population contient 22 allèles : 13 sont du type (A) et 9 sont du type (a).
II – Mesure de la variabilité génétique
1 – En se basant sur les phénotypes observés
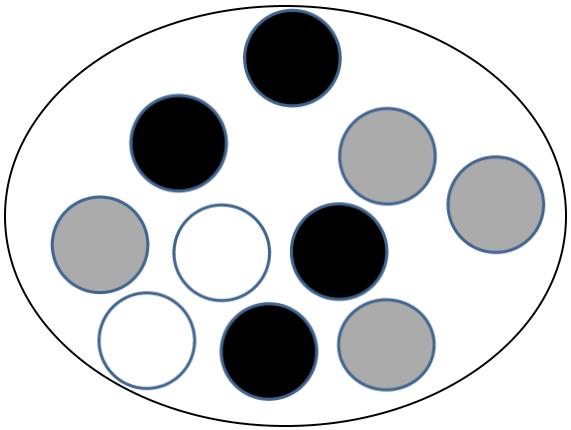
La figure suivante montre un schéma d’une population constitué de N = 10 individus.
On considère que la couleur du corps est contrôlée par un gène représenté par 2 allèles codominants (N responsable de la couleur noire) et (B responsable de la couleur blanche).
Q-1 – Calculez les fréquences des différents phénotypes.
Q-2 – Calculez les fréquences des différents génotypes.
Q-3 – Calculez les fréquences alléliques.

R-1 – Pour calculer la fréquence d’un phénotype, on applique la formule suivante :
Application numérique :
- f ([N]) = 4/10 = 0,4.
- f ([B]) = 2/10 = 0,2.
- f ([NB]) = 4/10 = 0,4.
NB : la somme des fréquences (0,4 + 0,2 + 0,4) = 1.
R-2 – Dans le cas de codominance, les fréquences des génotypes peuvent être déduites à partir des fréquences des phénotypes (parce que chaque phénotype est contrôlé par un génotype différent). Alors :
- f (NN) = f ([N]) = 4/10 = 0,4.
- f (BB) = f ([B]) = 2/10 = 0,2.
- f (NB) = f ([NB]) = 4/10 = 0,4.
R-3 – On peut calculer la fréquence des allèles par deux méthodes :
- Première méthode :
– Pour l’allèle (N) : on a 4 individus [N] qui portent 2 allèles (N) et 4 individus [NB] qui porte 1 allèle N. donc :
f (N) = (2 × 4 + 4) / 2 × 10 = 0,6.
– Pour l’allèle (B) : on a 2 individus [B] qui portent 2 allèles (B) et 4 individus [NB] qui porte 1 allèle B. donc :
f (B) = (2 × 2 + 4) / 2 × 10 = 0,4.
- Deuxième méthode :
f (allèle) = f (génotype homozygote pour cet allèle) + 1/2 × f (génotype hétérozygote)
– Pour l’allèle (N) : on a f (NN) = 0,4 et f (NB) = 0,4. donc : f (N) = 0,4 + 1/2 × 0,4 = 0,6.
– Pour l’allèle (B) : on a f (BB) = 0,2 et f (NB) = 0,4. donc : f (N) = 0,2 + 1/2 × 0,4 = 0,4.
NB : Dans le cas de la dominance complète, on ne peut pas calculer les fréquences des différents génotypes et des allèles à partir des fréquences des phénotypes. En effet, on ne peut pas différencier entre les génotypes (homozygote ou hétérozygote) des individus qui ont un phénotype dominant.
Par exemple, si on considère un gène représenté par deux allèles (A : dominant, et a : récessif). Pour les individus qui ont un phénotype dominant [A], on ne peut pas différencier entre ceux qui ont le génotype (AA) et ceux qui ont le génotype (Aa).
2 – La loi d'Hardy — Weinberg
a – La population théorique idéale
L’étude des variations génétiques de la population à travers les générations est difficile dans les populations naturelles à cause des facteurs susceptibles de modifier leur structure génétique. Pour cela, il est possible de suivre l’évolution des caractéristiques héréditaires dans une population théorique idéale qui présente les caractéristiques suivantes :
- Population d'organismes diploïdes à reproduction sexuée sans chevauchement entre les générations.
- Son nombre est infini et les croisements se font au hasard (panmixie), et leurs gamètes se rencontrent au hasard (pangamie).
- Fermée génétiquement (pas de migration).
- Ses individus ont la même capacité de se reproduire et la même capacité de donner des descendants capables de vivre.
- Absence de mutation et d’anomalies au cours de la séparation des chromosomes pendant la méiose (un individu Aa produira toujours 50 % de gamètes A et 50 % de gamètes a).
b – Démonstration de la loi H-W
Dans une population théorique-idéale, on considère un gène représenté par deux allèles : l’allèle (A) dominant, sa fréquence dans la population est p, et l’allèle (a) récessif, sa fréquence dans la population est q.
- Dans une génération initiale G0, on a :
Les fréquences des génotypes :
- f0 (AA) = D0.
- f0 (Aa) = H0.
- f0 (aa) = R0.
Les fréquences des allèles :
- f0 (A) = p0 = f0 (AA) + f0 (Aa) / 2 = D0 + H0 / 2.
- f0 (a) = q0 = f0 (aa) + f0 (Aa) / 2 = R0 + H0 / 2.
- Dans une génération G1 :
Les individus de cette génération sont issus de croisements entièrement aléatoires entre les individus adultes de la génération G0. L’échiquier ci-dessous représente l’ensemble des associations aléatoires entre gamètes porteurs d’allèles (A) ou (a) provenant des individus adultes ♂ ou ♀ de la génération G0.
Gamètes | A p0 | a q0 |
A p0 | AA (p0)² | Aa (p0q0) |
a q0 | Aa (p0q0) | aa (q0)² |
Alors :
- Les fréquences des différents génotypes dans la génération G1 sont :
- f1 (AA) = (p0)².
- f1 (Aa) = 2(p0q0).
- f1 (aa) = (q0)².
- Les fréquences des allèles A et a dans la génération G1 sont :
- f1 (A) = f1 (AA) + f1 (Aa) / 2 = (p0)² + 2(p0q0) / 2 = (p0)² + (p0q0) = p0 ( p0 + q0) = p0.
- f1 (a) = f1 (aa) + f1 (Aa) / 2 = (q0)² + 2(p0q0) / 2 = (q0)² + (p0q0) = q0 ( p0 + q0) = q0.
Donc : les fréquences alléliques à la génération G1 ne changent pas par rapport à la génération précédente (la population est en équilibre), et les fréquences génotypiques sont déterminées à partir des fréquences alléliques comme suit :
- f(AA) = p²
- f(Aa) = 2pq
- f(aa) = q²
Avec : f(AA) + f(Aa) + f(aa) = p² + 2pq +q² = (p+q)² = 1.
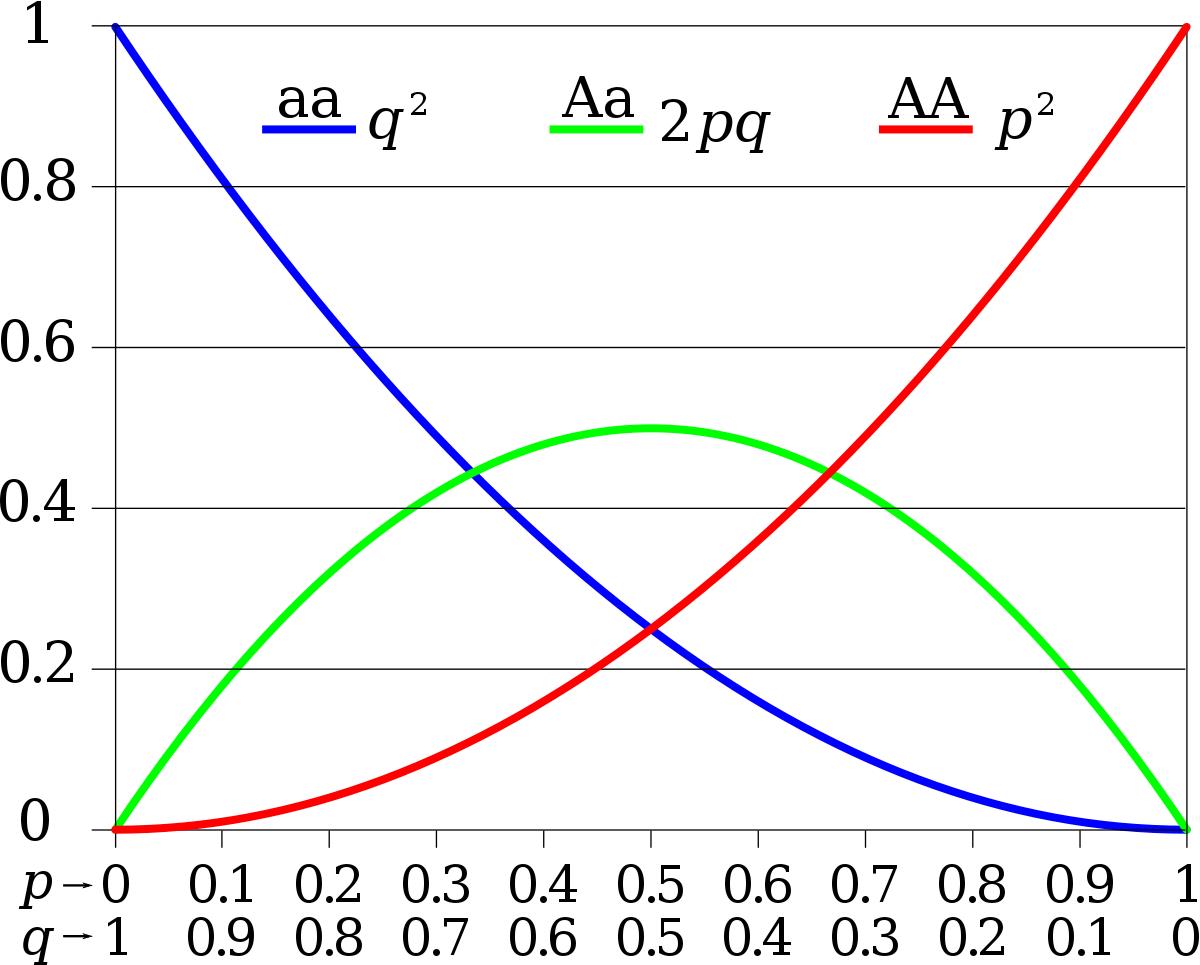
Bilan (loi de H-W) : Dans une population théorique idéale, les fréquences génotypiques et alléliques restent stables d’une génération à une autre.
La figure suivante montre la correspondance entre les fréquences alléliques et les fréquences génotypiques dans le cas d’un gène représenté par deux allèles (A et a) dans une population en équilibre de H-W.
Exercices d’applications :
I – Le phénotype de pigmentation alaire, chez une espèce de papillons, est gouverné par un gène existant sous deux formes alléliques, notées A et a, dont les fréquences sont p et q. Une première étude a montré que le phénotype clair est récessif et correspond au génotype aa. Le piégeage, en milieu naturel, d’une population de 500 papillons, a permis de dénombrer 480 phénotypes foncés et 20 clairs.
Q – En supposant que la population soit panmictique (soumise à la loi H-W), calculez les fréquences alléliques et génotypiques dans la population P0.
II – Le groupe sanguin Rhésus est codé par un gène autosomal à deux allèles : l’allèle Rh+ dominant responsable du groupe [Rh+], et l’allèle Rh récessif responsable du groupe [Rh-]. En 1970, une étude sur 400 individus dans la zone basque en Espagne a montré que 230 parmi eux sont de groupe [Rh+]. En supposant que la population étudiée soit soumise à la loi de Hardy–Weinberg :
Q – Calculez les fréquences des allèles et des génotypes.
c – Application aux maladies héréditaires liées au chromosome X
Dans une population équilibrée, on considère un gène à deux allèles (A et a) porté sur le chromosome sexuel X. Soit p la fréquence de l’allèle A et q la fréquence de l’allèle a.
- Chez les femelles, on a :
- f(XA XA) = p² ; f(XA Xa) = 2pq ; f(Xa Xa) = q².
- f(♀[A]) = f(XA XA) + f(XA Xa) = p² + 2pq ; f(♀[a]) = f(Xa Xa) = q².
- Chez les mâles on a :
- f(♂[A]) = f(XA Y) = f(A) = p.
- f(♂[a]) = f(Xa Y) = f(a) = q.
Conclusion : chez les femelles, les fréquences des génotypes sont conformes à la loi de H-W, alors que chez les mâles, les fréquences des génotypes sont celles des allèles.
Exercice d’application :
I – L’hémophilie B est une maladie héréditaire liée au chromosome X. L’allèle (h) responsable de cette maladie est récessif par rapport à l’allèle normal (H). Une étude réalisée chez une population a montré que l’incidence de cette maladie est de 1 sur 2000 naissances de garçons.
En considérant que la population étudiée est équilibrée :
Q – Calculez la fréquence de l’apparition de la maladie chez les mâles et chez les femelles. Que peut-on conclure ?
R – On sait que les fréquences alléliques d’une maladie liée à X sont les mêmes que les fréquences des génotypes des garçons. Ainsi :
- Chez les garçons :
- f([h]) = f(XhY) = q = 1/2000 = 0.0005.
- Chez les femmes :
- f([h]) = f(XhXh) = q² = (0.0005)² = 0.00000025.
- Donc la fréquence d’apparition d’une maladie récessive et liée à X est plus grande chez les garçons que chez les femmes.
II – La maladie d’Alport est une maladie héréditaire gouvernée par un gène porté par le chromosome X. L’allèle (A) responsable de cette maladie est dominant par rapport à l’allèle normal (a). Des études chez une population ont montré que la fréquence de l’allèle (A) est p = 0,087.
En considérant que la population étudiée est équilibrée :
Q – Calculez la fréquence de l’apparition de la maladie chez les mâles et chez les femelles. Que peut-on conclure ?
R –
- Chez les garçons :
- f([A]) = f(XAY) = p = 0.087.
- Chez les femmes :
- f([h]) = f(XAXA) + f(XAXa) = p² + 2pq = 0.0872 + 2x0.087x0.917 = 0.1664.
- Donc la fréquence d’apparition d’une maladie dominante et liée à X est plus grande chez les femmes que chez les hommes.
3 – Test de l’équilibre d’une population (Khi deux ou khi carré)
Pour déterminer si une population naturelle est en équilibre, on la compare à une population théorique idéale. Cette comparaison est facile pour des caractères co-dominants, pour lesquels le calcul des fréquences alléliques est possible.
On applique dans cette comparaison un test nommé test de khi 2 (X2). Qui est réalisé selon Les étapes suivantes :
On considère dans cet exemple un gène représenté par deux allèles (A) et (B), leurs fréquences sont respectivement (p) et (q).
- Calcul des fréquences alléliques réelles parmi les N individus échantillonnés.
- Calcul des effectifs génotypiques attendus dans une population théorique idéale qui q le même effectif et les mêmes fréquences alléliques que la population étudiée soit :
- Et (AA) = p²x N.
- Et (AB) = 2 pq xN.
- Et (BB) = q²xN.
- Comparaison des effectifs observés et des effectifs par un test statistique de Khi deux : X² = Σ ((Eo – Et) 2 / Et).Eo : effectifs génotypiques observés ; Et : effectifs génotypiques théoriques.
- La valeur X2 calculé est comparée à une valeur seuil, lue dans une table X2 en fonction de 2 paramètres :
- α : Risque d’erreur, choisi par l’expérimentateur, est souvent égale à 5 % (0.05).
- ddl : Degré de liberté (ddl = le nombre de génotypes – nombre d’allèles).
- Conclusion :
- Si X2 calculée est inférieure au seuil : la population est en équilibre selon la loi de H-W.
- Si X2 calculée est supérieure au seuil : la population n’est pas en équilibre.
Exercice d’application :
Chez l’Homme, le groupe sanguin MN est déterminé par un gène à deux allèles codominants M et N, ce qui permet d’attribuer un génotype à chaque individu échantillonné, puis d’estimer les fréquences alléliques dans la population.
Une étude portant sur 730 aborigènes australiens a donné les résultats suivants : [M] = 22 ; [N] = 492 ; [MN] = 216.
Q – La population étudiée est-elle en équilibre de H-W ? ( On prend α = 0.05).
R –
- Détermination des génotypes observés :
- Eo (MM) = Eo([M]) = 22.
- Eo (MN) = Eo([MN]) = 216.
- Eo (NN) = Eo([NN]) = 492
- Détermination des fréquences alléliques : soit p la fréquence de (M) et q la fréquence de (N) :
- f (MM) = f([M]) = 22 / 730 = 0.0301.
- f (MN) = f([MN]) = 216 / 730 = 0.2959.
- f (NN) = f([N]) = 492 / 730 = 0.674.
- p = f(M) = f(MM) + 1/2xf(MN) = 0.0301 + 0.5x0.2959 = 0.17805.
- q = f(N) = f(NN) + 1/2xf(MN) = 0.674 + 0.5x0.2959 = 0.82195.
- Détermination des génotypes théoriques :
- Et(MM) = p²x730 = 23.14.
- Et(NN) = q²x730 = 493.19.
- Et(MN) = 2pqx730 = 213.67.
- Calcule de la valeur de Khi deux :
- X2 = ((23.14-22)²/22) + ((493.19-492)²/492) + ((213.67-216)²/216) = 0.62.
- Conclusion : la valeur calculée est plus petite que le seuil (3.841), donc la population étudiée est en équilibre de H-W.
III – Les facteurs de variation de la population
1 – Les mutations
Une mutation au sens large est toute modification de quantité de l’information génétique ou de la structure de son support (gène et chromosomes). Une mutation peut être ponctuelle ou chromosomique :
- Les mutations ponctuelles sont des modifications au niveau des nucléotides.
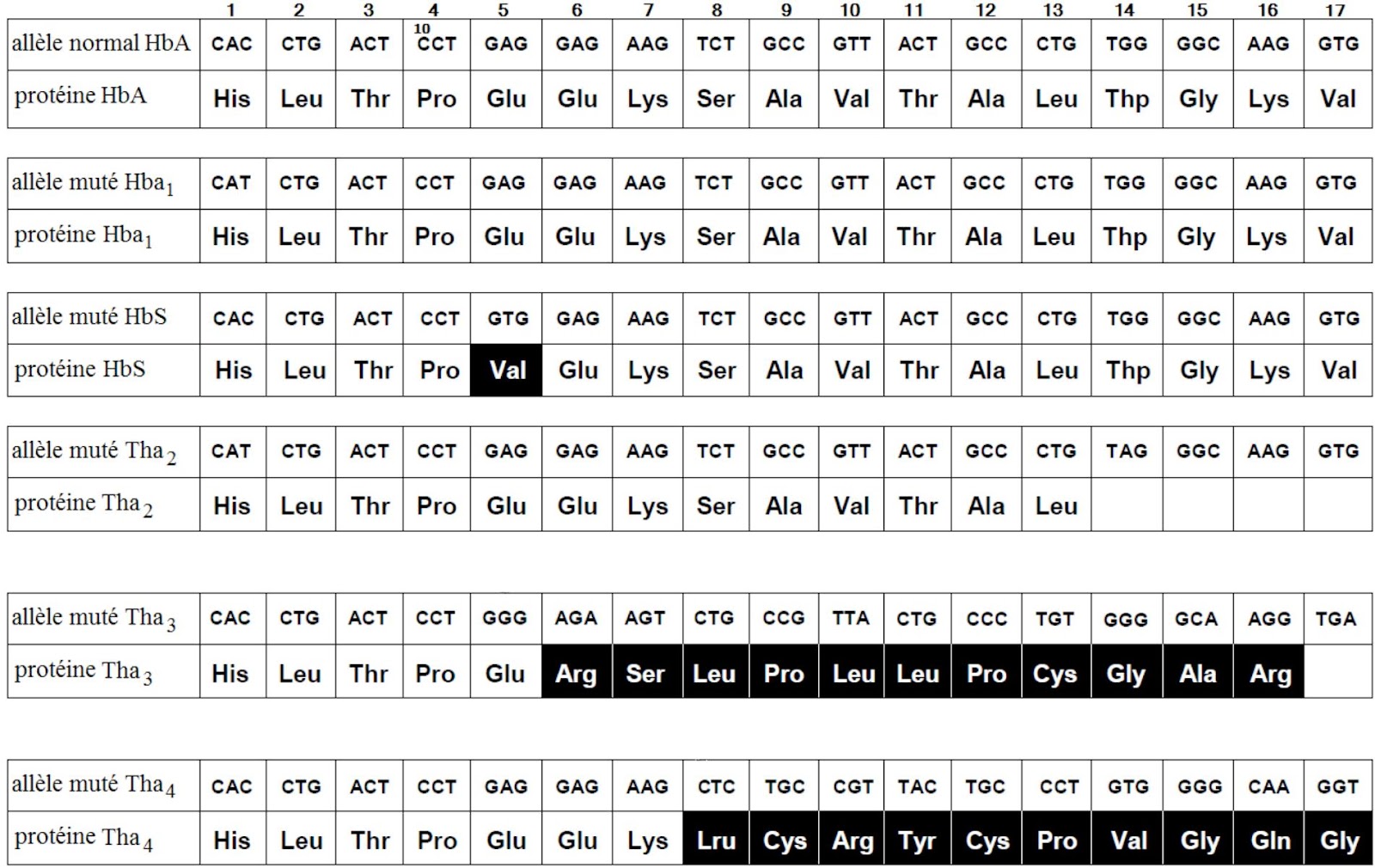
Exemple : Le β-globuline est un polypeptide qui entre dans la composition de l’hémoglobine. Chez l’Homme, la synthèse du β-globuline est gouvernée par un gène polyallélique : un allèle normal nommé HbA et plusieurs allèles mutés responsables de certaines anémies. Les figures ci-dessous représentent des séquences de nucléotides des différents allèles (brins non transcrits) du gène β – globuline, ainsi que les protéines qui résultent de l’expression de ces allèles.
Q – Complétez le tableau suivant
Allèle | Type de mutation | Changement au niveau de l’allèle | Changement au niveau de la protéine |
Hba1 | | | |
HbS | | | |
Tha2 | | | |
Tha3 | | | |
Tha4 | | | |
R- Le tableau
Allèle | Type de mutation | Changement au niveau de l’allèle | Changement au niveau de la protéine |
Hba1 | Substitution | Substitution de C par T dans le triplet 1 | Aucun changement = mutation silencieuse |
HbS | Substitution | Substitution de A par T dans le triplet 5 | Changement de l’acide aminé 5 (Val au lieu de Glu) |
Tha2 | Substitution | Substitution de G par A dans le triplet 14 | Arrêt de la formation de la protéine |
Tha3 | Délétion | Délétion de A au niveau le triplet 5 | Changement de plusieurs acides aminés après la mutation |
Tha4 | Addition | Addition de C au niveau du triplet 8 | Changement de plusieurs acides aminés après la mutation |
- Les mutations chromosomiques : ce sont des mutations induisant la modification du nombre ou de la structure des chromosomes, entraînant une maladie génétique ou la mort. La figure suivante présente des mutations de structure de chromosomes.
Conclusion : Les mutations ponctuelles constituent le seul mécanisme génétique pouvant créer de nouveau allèles participant ainsi à la diversité du pool génétique des populations. Or une mutation est un phénomène génétique rare (10-4 à 10-8) et son effet sur les populations n’apparaît qu’après plusieurs générations et accumulations de plusieurs mutations.
Quant aux mutations chromosomiques, elles causent souvent des maladies génétiques, la stérilité ou la mort des individus qui n’ont alors plus la possibilité de transmettre leurs allèles.
2 – La sélection naturelle
a – Notion de la sélection naturelle

Données expérimentales : la phalène du bouleau est un papillon nocturne qui est caractérisé par deux sous-espèces (Biston blatularia et Biston carbonaria). Pendant le jour, les phalènes s’immobilisent sur les troncs d’arbres ; elles sont alors des proies faciles pour les oiseaux.
Jusqu’au milieu du 19ᵉ siècle, avant l’industrialisation massive, les populations de phalènes du bouleau étaient composées, en Angleterre, exclusivement de la sous-espèce claire
Après l’industrialisation qui a eu lieu en Angleterre, un recensement du début du 20ᵉ siècle a mis en évidence que l’importance relative de ces deux phénotypes a fluctué au cours du temps dans les régions rurales et industrielles. La sous-espèce claire était majoritaire dans les régions rurales et la sous-espèce foncée était quant à elle largement majoritaire dans les régions industrielles.
En 1955, H. Kettlewell a effectué L’expérience suivante :
– Au début de l’expérience, des phalènes des 2 phénotypes sont marqués d’une petite tache de peinture, puis lâchées :
- dans un bois dont les arbres sont sombres, car pollués par la suite (Birmingham).
- dans un milieu rural (Dorset) dans un bois où les arbres sont clairs (car couverts de lichen).
– À la fin de l’expérience, les papillons survivants sont recapturés puis dénombrés. Les résultats sont présentés dans le tableau suivant.
| Papillons Lâchés (%) | Papillons recapturés (%) | ||
Papillons clairs | Papillons sombres | Papillons clairs | Papillons sombres | |
Birmingham | 29 | 71 | 16 | 84 |
Dorset | 49 | 51 | 75 | 26 |
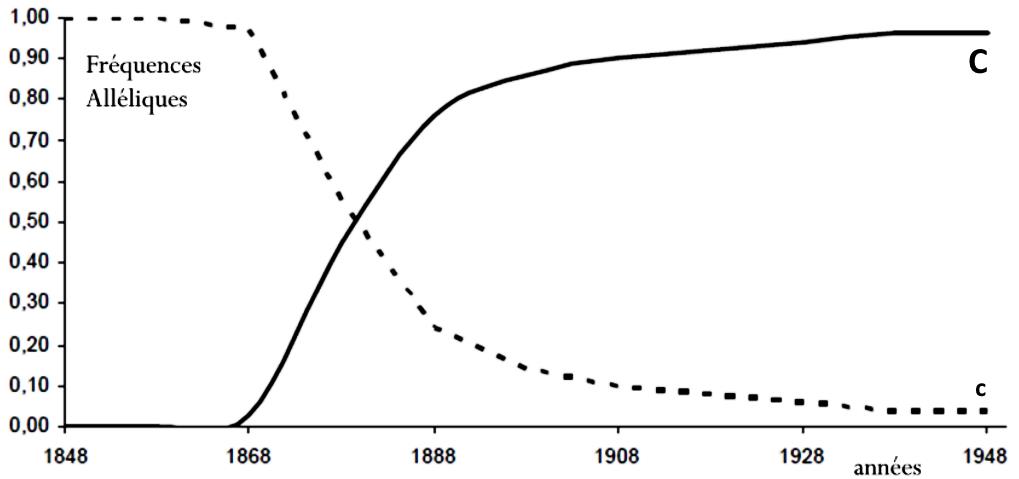
La figure suivante montre la variation des fréquences des allèles C (responsable de la couleur sombre) et c (responsable de la couleur claire) dans la région de Birmingham.
Q-1 – Décrivez les résultats du tableau.
Q-2 – Expliquez ces résultats, puis proposez une définition du mécanisme responsable des changements observés.
Q-3 – Expliquez la variation des fréquences des allèles (C et c) observée dans la région de Birmingham.
R-1 – Dans la région polluée (Birmingham) les troncs d’arbres sont sombres, et on constate que le pourcentage des papillons sombres est plus grand que celui des papillons clairs. Alors que l’inverse est constaté dans la région non polluée (Dorset).
R-2 – Dans les régions polluées, les troncs d’arbres sont devenues sombres, ce qui a rendu les papillons clairs facilement visibles par les oiseaux prédateurs. Ainsi, elles sont exposées à la prédation.
En revanche, dans les régions polluées, les troncs d’arbres sont restés de couleur claire, ce qui a permis aux papillons clairs de rester invisibles, et donc non exposées à la prédation.
Les papillons ont donc été sujets à une sélection naturelle exercée par les oiseaux prédateurs qui arrivent de les distinguer grâce à leur phénotype et selon l’environnement (tronc d’arbre).Ainsi, les papillons sombres subissent une sélection positive dans la région polluée et une sélection négative dans la zone non polluée, et l’inverse pour les papillons clairs.
Définition : La sélection naturelle désigne l’ensemble de phénomènes qui induisent chez les organismes vivants des différences dans le succès reproductif (la survie et la contribution dans les croisements) selon les caractères portés par ces organismes. Ces mécanismes sélectionnent donc au fil des générations certains caractères (donc génotypes) plutôt que d’autres.
R-3 – Les papillons sombres porteurs de l’allèle C sont mieux camouflés dans la région de Birmingham. Alors, ils échappent aux prédateurs et contribuent plus aux croisements, et donc à la formation des générations suivantes. Ainsi, la fréquence de l’allèle C augmente graduellement au détriment du déclin de l’allèle sauvage c.
b – Les différents types de sélection naturelle
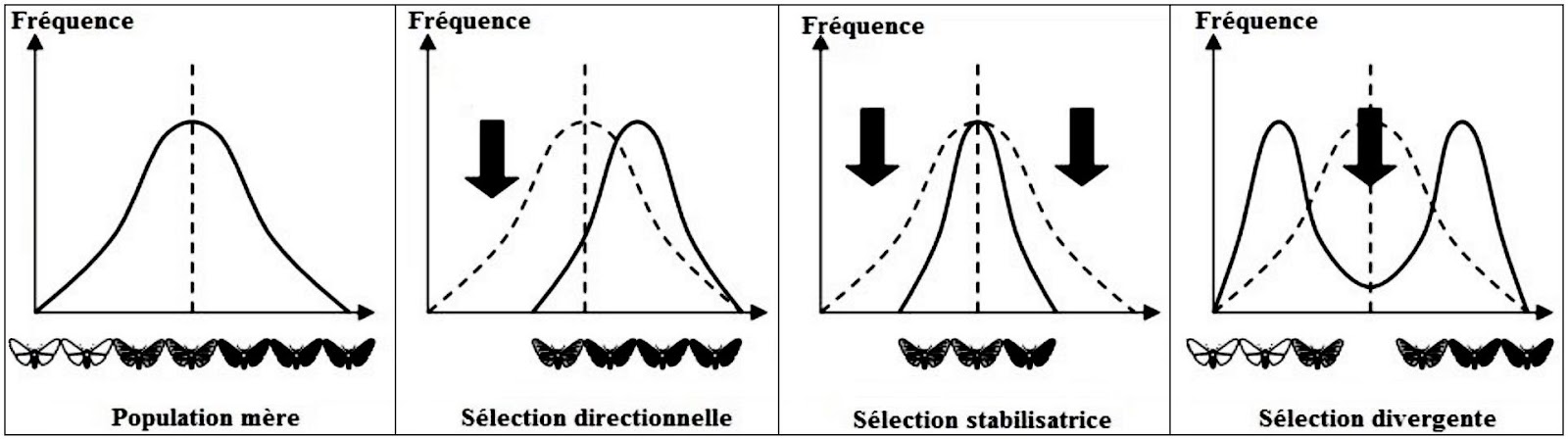
La figure suivante représente les différents types de la sélection naturelle.
Il existe 3 sortes de sélection naturelle :
- Sélection directionnelle : favorise les phénotypes situés à une seule extrémité de la courbe.
- Sélection divergente : favorise les deux phénotypes extrêmes et élimine celui du centre, rendant la distribution bimodale.
- Sélection stabilisante : ce type de sélection favorise les phénotypes de centre de la distribution et élimine ceux des extrémités.
3 – La dérive génétique
Pour comprendre l’influence de la dérive génétique sur la population, on propose l’étude des données suivantes :
Les Huttérites sont les membres d’une secte qui, persécutés en Europe, se sont installés en Amérique du Nord au dix-neuvième siècle. Comme les Amish, ils ont établi une série de colonies d’une centaine d’individus dans lesquelles ils vivent en autarcie sans se marier avec les personnes étrangères.
Mc Lellan et ses collaborateurs y ont étudié la fréquence de certains allèles des groupes sanguins des systèmes ABO. Le tableau ci-dessous représente les résultats obtenus.
| Groupes sanguins (%) | |
| A | B |
Europe, USA | 14,5 à 25 | 6 à 14,5 |
Huttérites | 35 | 2 |
Amish | 66 | 6,5 |
Q-1 – Analysez le tableau.
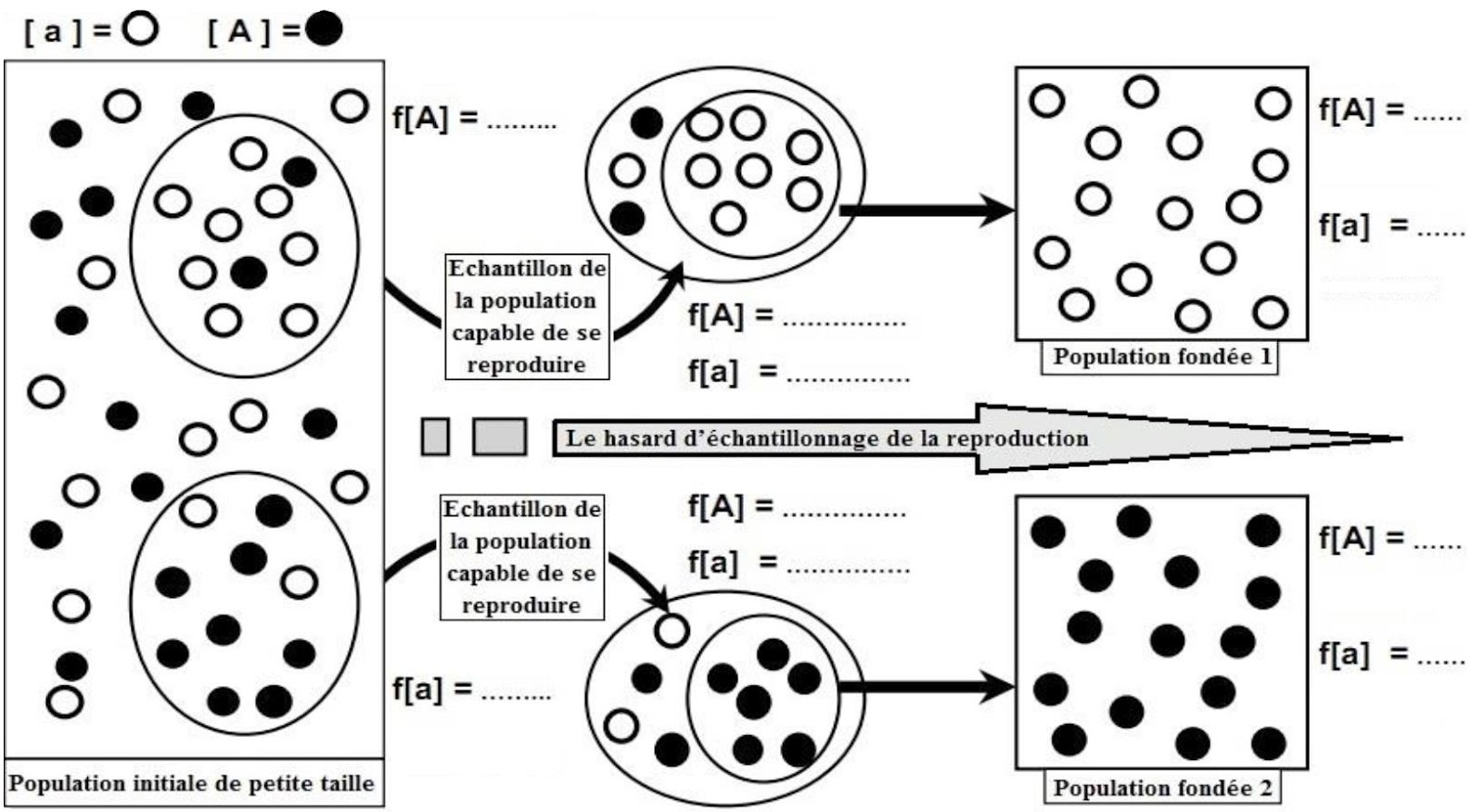
Mc Lellan et ces collaborateurs ont expliqué l’évolution de la structure génétique des Huttérites par la dérive génétique, pour mettre en évidence l’effet de ce phénomène sur cette population, on vous propose le schéma ci-dessous qui représente un modèle explicatif.
Q-2 – Calculez les différentes fréquences de phénotype dans ces populations.
Q-3 – Discutez les résultats obtenus en expliquant comment intervient le phénomène étudié à l’évolution de la structure génétique de la population.
Q-4 – En se fondant sur les données précédentes et les résultats obtenus, expliquez l’origine du changement de la structure génétique des Huttérites et des Amish.
R-1 – Amish et Huttérites présentent des fréquences très différentes des moyennes constatées dans les populations européennes et nord-américaines.
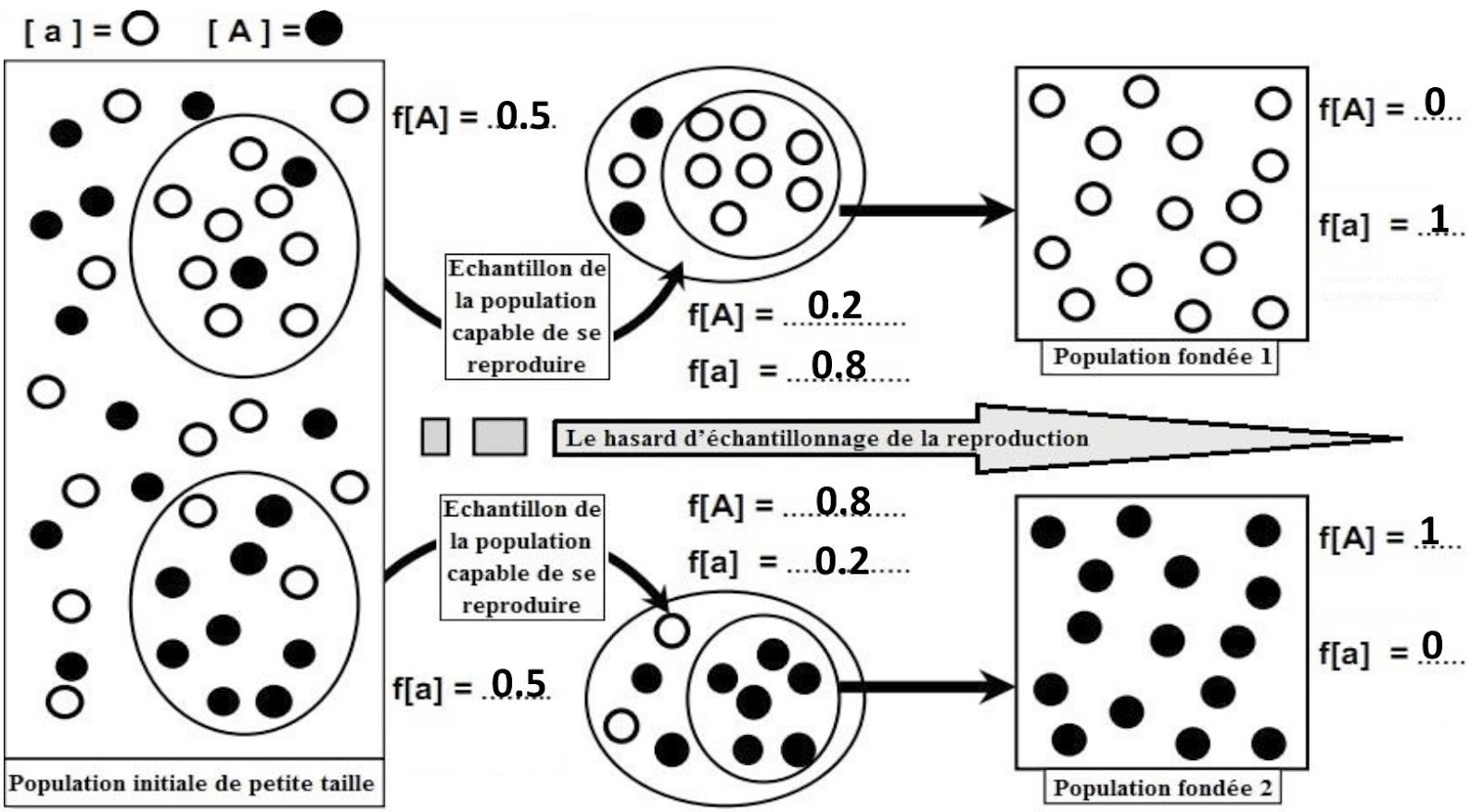
R-2 –
R-3 – C’est le hasard d’échantillonnage reproductif qui entraîne, chez la population fondée (1), le croisement des individus [a] entre eux, provoquant l’élimination du phénotype [A] à la seconde génération en fixant le phénotype [a], et l’inverse chez la population fondée (2).
R-4 – La population secte (Amish et Huttérites) descend sans doute d’un petit nombre d’individus ayant migré d’Europe (population d’origine) ne transportant avec eux qu’une partie de la diversité génétique des populations d’Europe. C’est que l’on appelle l’effet fondateur. Le temps passant, il se produira certainement dans cette population des fluctuations de fréquences qui n’existeront pas en Europe et en Amérique du Nord.
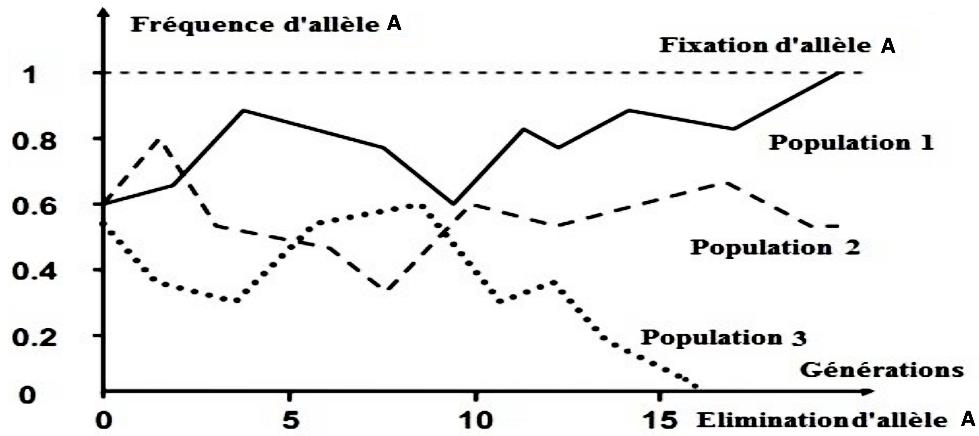
Exercice d’application : le graphe suivant représente l’évolution de la fréquence de l’allèle (A) à travers les générations chez 3 populations de petite taille, en utilisant la modélisation assistée par le système information.
Q-1 – Quel phénomène exprimé par le graphe ?
Q-2 – À partir de l’analyse du graphique, déterminez les aspects de ce phénomène et leur effet sur la structure génétique de la population.
R-1 – Puisqu'on constate sur le graphe des fluctuations aléatoires de la fréquence allélique chez les populations de petite taille. Donc, le phénomène exprimé par ce graphe est la dérive génétique.
R-2 – D’après le graphique, on constate que la fréquence de l’allèle A atteint aléatoirement la valeur 1, chez la population 1, dans ce cas, on parle de la fixation de l’allèle A chez cette population. Alors que chez la population 3 on observe le contraire, élimination de l’allèle A.
4 – La migration
La migration ou flux génique correspond aux échanges d’individus (d’allèles) entre populations de même espèce, géographiquement séparées. Il existe plusieurs modèles de migration :
a – Modèle unidirectionnel (continent – île)
Pour comprendre l’effet de la migration unidirectionnel sur la variabilité génétique des populations, on propose l’étude des données suivantes :
Aux États-Unis, en vérité, mais non en droit, tout enfant issu d’un couple mixte est considéré comme appartenant à la communauté noire. De ce fait, le transfert de gènes ne peut s’effectuer que des blancs vers les noirs et jamais en sens inverse (transfert unidirectionnel de gènes).
Une étude célèbre faite par Glass et Li en 1953 ; ils ont choisi d’étudier l’allèle Ro du système rhésus, car il est très rare en Europe et très fréquent en Afrique à l’origine des noirs américains. Le tableau suivant donne l’estimation de la fréquence de cet allèle d’après cette étude.
La fréquence de l’allèle Ro | |||
En 1953, dans la communauté noire des États-Unis | Dans les diverses populations origines esclaves (valeur moyenne actuelle) | Dans les populations européennes qui ont migré vers les États-Unis | Dans la communauté blanche des États-Unis |
0,0446 | 0,63 | 0,028 | 0,028 |
Q-1 – Comparez les données du tableau, que peut-on déduire ?
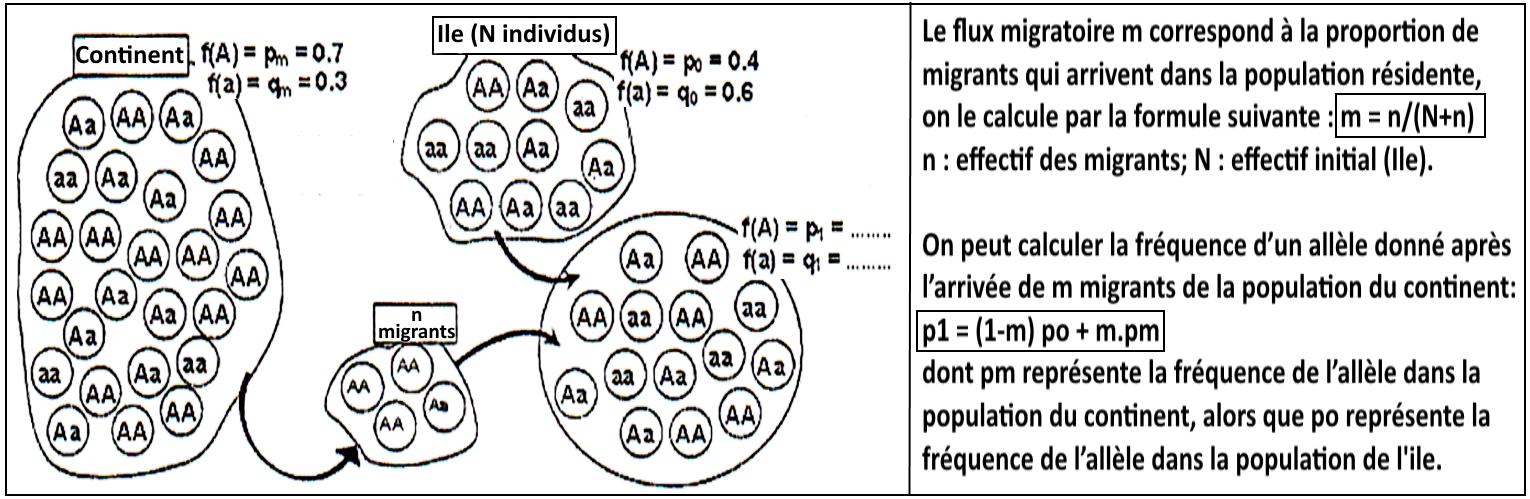
Pour expliquer l’origine de l’évolution de la structure génétique de la communauté noire des États-Unis, on vous propose le modèle de migration le plus simple, appelé modèle insulaire, est celui où les échange d’individus s’effectuent dans un seul sens avec un flux de gènes unidirectionnel entre une population 1 de grande taille (le continent) et une population 2 de petit effectif (l'île), la figure suivante représente ce modèle.
Q-2 – En utilisant les données de la figure 2 et le modèle proposé sur la figure 1, calculez le flux migratoire (m) et la fréquence de l’allèle (A) et de l’allèle (a) chez la population 2 après la migration.
Q-3 – Sachant que la structure génétique de la population de continent reste stable, que peut-on déduire sur la structure génétique de l’île ?
Q-4 – Montrez l’influence de la migration sur la variation de la structure génétique de la population noire américaine ?
R-1 – On constate que la fréquence de l’allèle Ro chez la communauté noire des États-Unis est faible par rapport à celle de la population origine des esclaves. Il est aussi plus grand que sa fréquence chez la communauté blanche des États-Unis (qui reste la même que la population européenne).
R-2 – f(A) = p1 = 0,48 ; f(a) = q1 = 0,52.
R-3 – On constate que la fréquence de l’allèle (A) augmente chez la population de l’île après la migration, si la migration poursuit avec le temps, la structure génétique de l’île devient la même que celle du continent.
R-4 – On peut expliquer la variation de la structure génétique de la communauté noire des États-Unis par la migration unidirectionnelle dont le transfert de gènes ne peut s’effectuer que des blancs vers les noirs et jamais en sens inverse (transfert unidirectionnel de gènes). Ce qui entraîne une variation des caractéristiques génétiques de la population noire sans modifier la structure génétique de la population d’origine.
b – Modèle multidirectionnel (modèle insulaire)
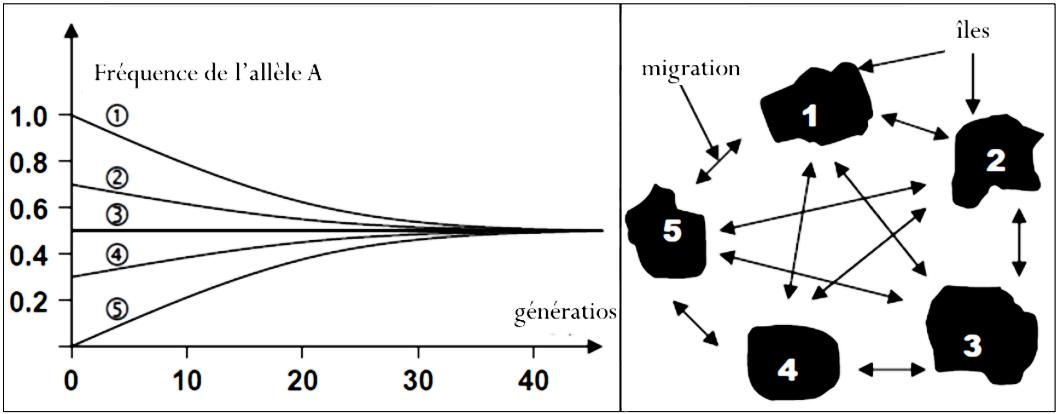
Le modèle archipel correspond à l’ensemble d’îles interconnectées par des échanges de migrants dans toutes les directions possibles avec des conséquences sur l’ensemble des populations. La figure suivante représente le modèle archipel de migration multidirectionnelle de 5 populations, le graphe montre l’évolution de la fréquence de l’allèle A chez ces 5 populations suite au flux migratoire multidirectionnel.
Q – Décrivez le graphique, que déduisez-vous ?
R – Au début, la fréquence de l’allèle A est très différente entre les 5 populations, et sous l’effet de flux migratoire multidirectionnel, les différences de fréquence alléliques entre les populations diminuent progressivement. Les populations convergent vers une fréquence allélique commune qui correspond à la moyenne des fréquences alléliques dans ces populations.
Ainsi, selon ce modèle, il y a une convergence vers l’homogénéité génétique entre les populations. Les différences de fréquences alléliques diminuent avec les générations et finissent par disparaître.
IV – Notion de l’espèce.
1 – Les critères caractérisant l’espèce
Il existe plusieurs critères sur lesquels on se base pour déférence entre les différentes espèces, citant comme exemples :
- Critère morphologique.
- Critères écologiques.
- Critères physiologiques.
- Critères d’interfécondité et la descendance féconde. Représente le critère le plus important pour déterminer l’espèce.
2 – Définition de l’espèce
Une espèce est une population ou un ensemble de populations dont les individus présentent plusieurs similarités (morphologique, physiologiques…), et qui peuvent effectivement ou potentiellement se reproduire entre eux et engendrer une descendance viable et féconde, dans des conditions naturelles