SM
Normale
2016
2
Contenu de l'examen :
Partie I : Restitution des connaissances (5 points)(Unité 4)
I – Répondez, sur votre feuille de production, aux questions suivantes :
a – Définissez : La population – La dérive génétique. (1 pt)
b – Citez deux caractéristiques de la population théorique idéale (population en équilibre selon la loi de Hardy – Weinberg). (0, 5 pt)
II – Recopiez, sur votre feuille de production, la lettre correspondante à chaque proposition parmi les propositions suivantes, puis écrivez devant chaque lettre « Vrai » ou « Faux ». (2 pts)
a – Le pool génique d’une population est l’ensemble des génotypes et des caractères phénotypiques (des phénotypes) des individus qui lui appartiennent.
b – Dans une population à effectif réduit, la dérive génétique réduit la diversité génétique.
c – Malgré leur trop faible probabilité, les mutations sont source de diversité génétique, au fil des générations.
d – Les mutations qui affectent les cellules somatiques sont des mutations héréditaires.
III – Pour chacune des données numérotées de 1 à 3, il y a une seule suggestion correcte. Recopiez, sur votre feuille de production, les couples ci-dessous et adressez à chaque numéro la lettre qui correspond à la suggestion correcte. (1.5 pt) (1,…) ; (2,…) ; (3,…).
1 – La sélection naturelle entraîne la modification génétique d’une population sous l’effet :
a : des facteurs environnementaux.
b : de la dérive génétique.
c : des facteurs mutagènes.
d : des croisements aléatoires.
2 – La mutation chromosomique est due à :
a : des modifications de la structure ou du nombre des chromosomes.
b : une substitution d’un seul nucléotide au niveau du chromosome.
c : une addition d’un seul nucléotide au niveau du chromosome.
d : une délétion d’un seul nucléotide au niveau du chromosome.
3 – Dans le cas d’une codominance non liée au sexe au sein d’une population donnée:
a : la fréquence des allèles est égale à la fréquence des génotypes.
b : la fréquence des phénotypes est égale à la fréquence des génotypes.
c : la fréquence des phénotypes est différente de la fréquence des génotypes.
d : la fréquence des allèles est égale à la fréquence des phénotypes.
Correction
I –
a – Exemples de définitions correctes :
La population : c’est un ensemble d’individus de la même espèce, qui occupent le même milieu et qui peuvent se croiser entre eux. (0.5 pt)
La dérive génétique : c’est une modification aléatoire de la fréquence des allèles, d’une génération à l’autre. Elle entraîne une diminution de la diversité génétique au sein d’une population. (0.5 pt)
b – Deux conditions parmi : (0.5 pt)
Reproduction sexuée et organismes diploïdes.
Générations non chevauchantes.
une population de grande taille.
Absence de migration.
Absence de sélection naturelle.
II – (a ; faux) – (b ; vrai) – (c ; vrai) – (d ; faux) 2 pts
III – (1 ; a) – (2 ; a) – (3 ; b) 1.5 pt
Partie II : Raisonnement scientifique et communication écrite et graphique (15 points)
Exercice 1 : (6 points)(Unité 3)
Afin de mettre en évidence le rôle de la méiose et de la fécondation dans le maintien de la stabilité du caryotype (formule chromosomique) et dans la diversité des phénotypes au cours des générations, on propose les données suivantes :
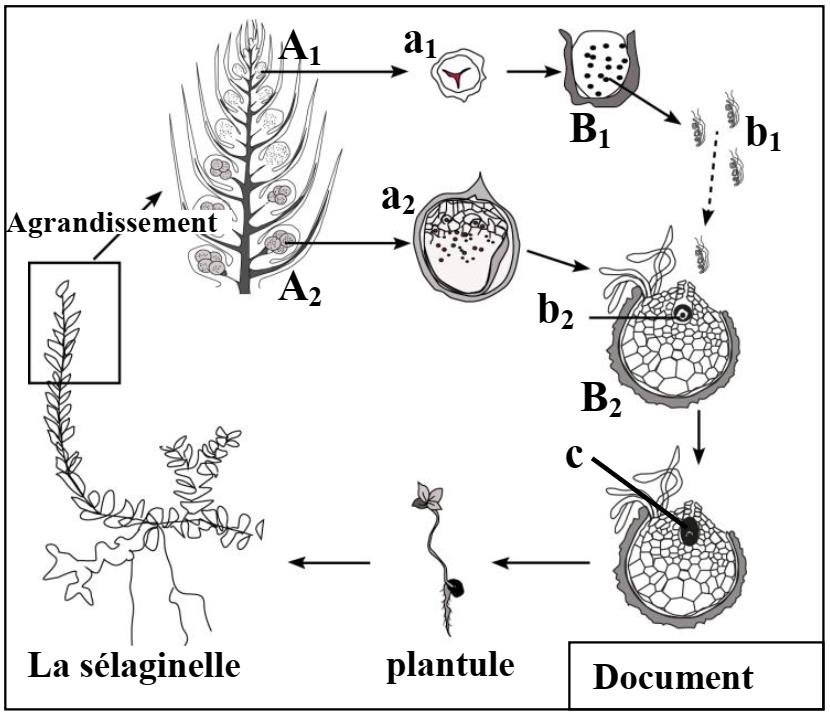
I. Les Sélaginelles sont de petites plantes des pays chauds ayant l’aspect de petites Fougères. Les sommets fertiles sont des épis dont les feuilles supérieures portent deux sortes de sporanges : microsporanges A1 et macrosporanges A2. Au sein de chacun des sporanges A1 et A2, des cellules mères diploïdes donnent naissance, respectivement, à des spores haploïdes a1 et a2. Les spores a1 et a2 protégées par une membrane épaisse, germent sur le sol humide et donnent, respectivement, des prothalles B1, d’où s’échappent les cellules flagellées b1, et des prothalles B2 renfermant chacune une volumineuse cellule b2. Une des cellules b1 nage, dans des gouttelettes d’eau sur la surface du sol, pénètre dans le col du prothalle B2 et s’unit à la cellule b2. La cellule c résultante de cette union se multiplie sur place et donne une jeune Sélaginelle. Le document ci-contre représente le cycle de développement de cette plante.

1 – Déterminez, en justifiant votre réponse, le phénomène biologique qui s’effectue au niveau des sporanges A1 et A2 d’une part et au niveau du prothalle B2 d’autre part. (1.25 pt)
2 – Représentez schématiquement le cycle chromosomique de cette plante et déterminez le type de ce cycle. (1 pt)
II. Pour étudier le mode de transmission de quelques caractères héréditaires non liés au sexe, on réalise le croisement de deux variétés de plantes du Pois de senteur : la première à fleurs pourpres et grains de pollen longs ; la seconde à fleurs rouges et grains de pollen ronds. Les deux variétés sont de lignées pures. On obtient en F1 une génération constituée uniquement de plantes à fleurs pourpres et grains de pollen longs.
3 – Que peut-on déduire à propos des résultats obtenus en F1 ? Justifiez votre réponse. (1 pt)
4 – A l’aide d’un échiquier de croisement, donnez les proportions des phénotypes attendus lors du croisement des hybrides F1 entre eux selon la troisième loi de Mendel (loi de la ségrégation indépendante des caractères). (2 pts)
Utilisez les symboles suivants :
R et r pour les allèles du gène responsable de la couleur de la fleur ;
L et pour les allèles du gène responsable de la forme des grains de pollen.
Afin de mettre en évidence l’exception de la troisième loi de Mendel, on exploite les travaux de Bateson et Punett réalisés en 1900. Ces derniers ont laissé se reproduire les hybrides de F1 entre eux. Le tableau ci-dessous représente les résultats obtenus en F2.
| Phénotypes des individus | Nombre d’individus | Pourcentage des phénotypes |
| Fleurs pourpres et grains de pollen longs | 4831 | 69.49% |
| Fleurs pourpres et grains de pollen ronds | 390 | 5.61% |
| Fleurs rouges et grains de pollen longs | 393 | 5.65% |
| Fleurs rouges et grains de pollen ronds | 1338 | 19.24% |
5 – Comparez ces résultats avec ceux obtenus en répondant à la question numéro 4. Que peut-on conclure à propos du mode de transmission de ces deux caractères ? (0.75 pt)
Correction
1 –
Sporange A1 : la méiose ; (0.25 pt)
Sporange A2 : la méiose ; (0.25 pt)
Justification : les cellules mères diploïdes donnent des cellules haploïdes (0.25 pt)
Prothalle B2 : la fécondation ; (0.25 pt)
Justification : l’union des deux gamètes mâle et femelle (0.25 pt)
2 –
L’établissement d’un cycle chromosomique correct (0.75 pt)
cycle haplo-diplophasique (0.25 pt)
3 –
Cas de dihybridisme (0.25 pt)
Les parents sont de lignées pures, F1 est uniforme. Vérification de la première loi de Mendel (0.25 pt)
Dominance absolue :
L’allèle responsable de la couleur pourpre est dominant (R) et l’allèle responsable de la couleur rouge est récessif (r) (0.25 pt)
L’allèle responsable des grains de pollen longs est dominant (L) et l’allèle responsable des grains de pollen ronds est récessif (l) (0.25 pt)
4 –
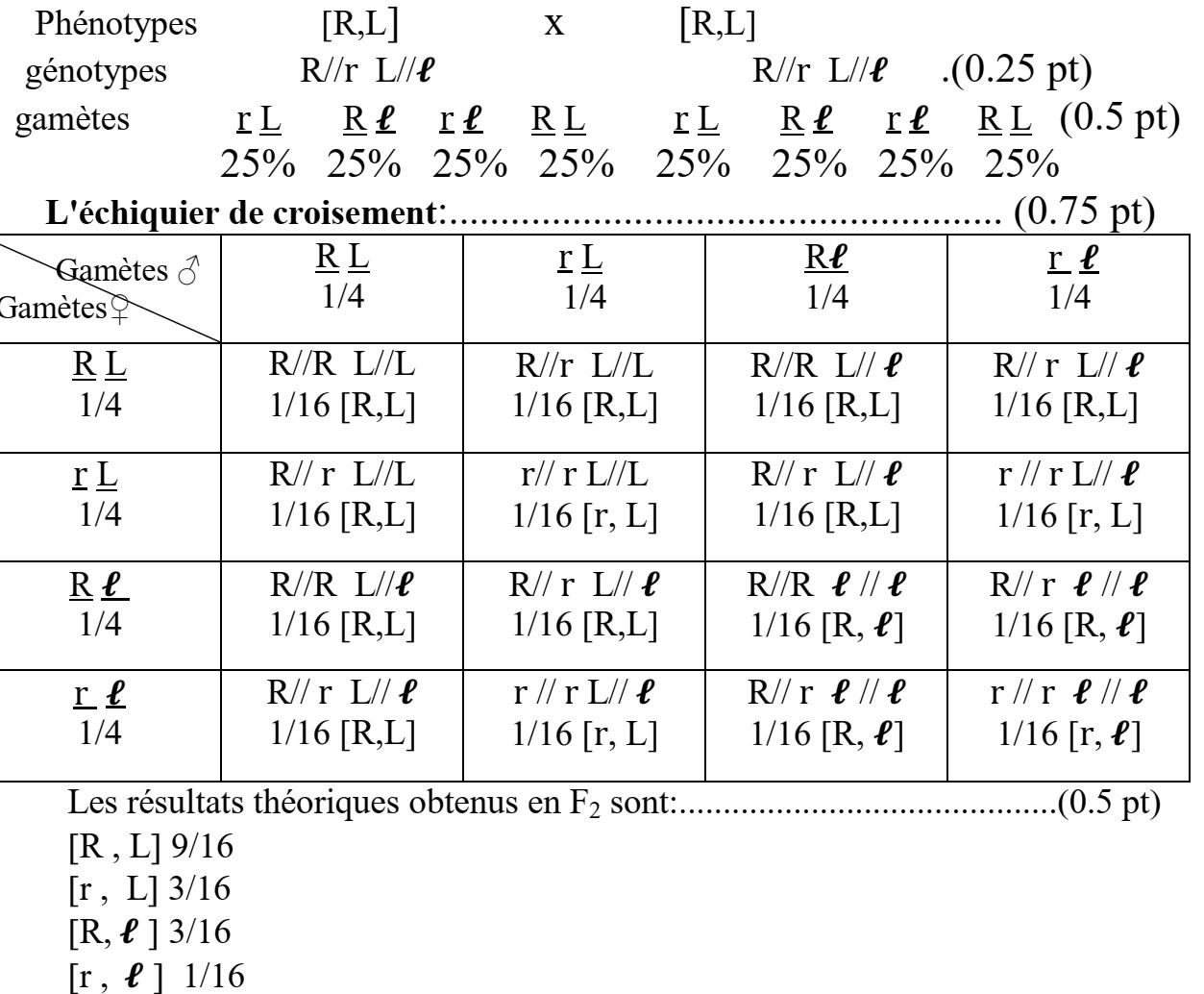
5 –
Les résultats obtenus par Punett et Bateson ne sont pas conformes aux résultats théoriques selon la troisième loi de Mendel (0.25 pt)
Déduction : les deux gènes sont liés (0.5 pt)
Exercice 2 : (4 points)(Unité 3)
La myopathie de Duchenne est une maladie héréditaire liée au sexe, elle débute dès l’enfance et se traduit par la dégénérescence progressive des fibres musculaires (muscles squelettiques et muscles respiratoires…), elle aboutit généralement à la mort avant la puberté. Le document 1 représente l’arbre généalogique d’une famille où s’exprime la myopathie de Duchenne.
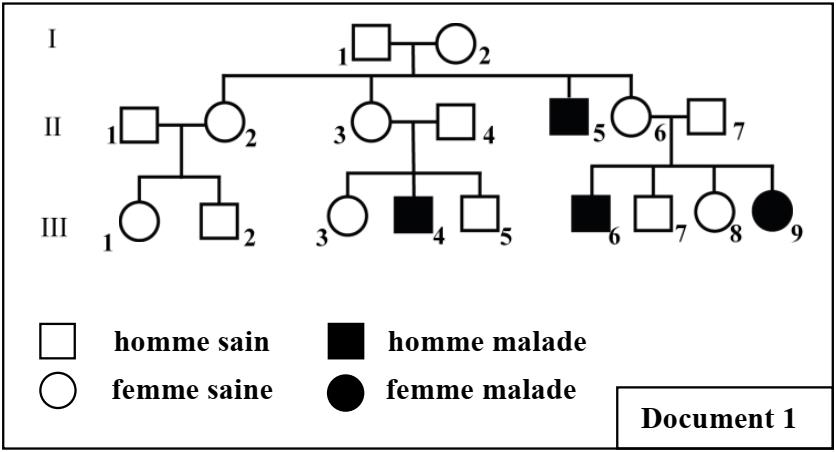
1 – En exploitant les données de l’arbre généalogique :
a – Déterminez le mode de transmission de cette maladie. Justifiez votre réponse. (1 pt)
b – Donnez les génotypes des parents II6 et II7, puis montrez que l’apparition de la myopathie chez la fille III9 est imprévisible. (1.5 pt)
(Utilisez M pour l’allèle dominant et m pour l’allèle récessif)
Pour chercher la cause de la myopathie chez la fille III9, on a réalisé son caryotype qui figure dans le document 2.
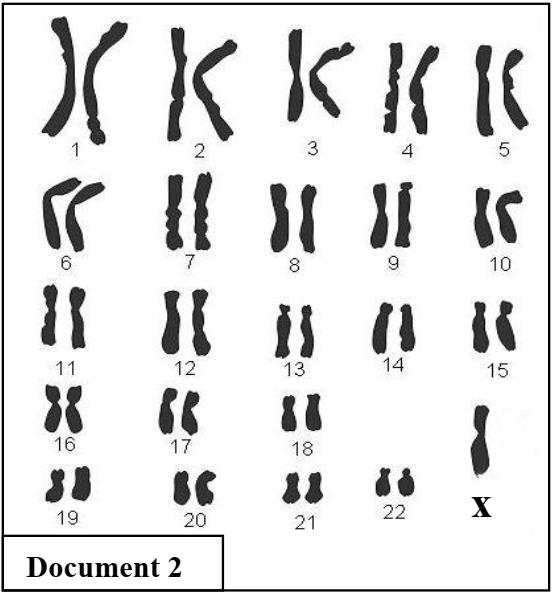
2 – En exploitant le document 2, déterminez le type d’anomalie chromosomique observée chez la fille III9 puis expliquez pourquoi elle est atteinte de la myopathie de Duchenne. (1.5 pt)
Correction
1-a –
Puisqu’un couple normal a donné naissance à un enfant malade, le gène responsable de la myopathie est récessif (0.5 pt)
Le gène responsable de cette maladie est porté par le chromosome sexuel X. Une seule justification parmi : (0.5 pt)
L’apparition de la maladie chez les garçons issus d’un père sain.
La fille III9 est malade
1-b –
Génotype de la mère II6 : XMXm (0.25 pt)
Génotype du père II7 : XMY (0.25 pt)
Le gène responsable de la maladie est récessif et porté par le chromosome sexuel X. Pour qu’une fille soit malade, elle doit être homozygote pour l’allèle muté, cela veut dire qu’elle doit recevoir une version de cet allèle de son père. Dans ce cas l’atteinte de la fille III9 est imprévisible, car son père est sain. (1 pt)
2 –
la fille est atteinte de la maladie de Turner, car son caryotype montre un seul chromosome sexuel X (0.25 pt)
Explication de l’atteinte de la fille par la maladie :
la fille III9 a reçu l’allèle responsable de la maladie de sa mère (0.25 pt)
la fille III9 n’a pas reçu le chromosome sexuel XM de son père à cause d’une anomalie chromosomique lors de la méiose (0.5 pt)
chez la fille III 9, l’absence de l’allèle dominant (l’allèle normal) a permis l’expression de l’allèle responsable de la maladie et par conséquent l’apparition de la myopathie chez elle (0.5 pt)
Exercice 3 : (5 points)(Unité 4)
Afin de favoriser l’amélioration de la longueur du tube de la corolle chez Longiflora (plante angiosperme), on a eu recours à la technique de la sélection artificielle, qui consiste à isoler les individus caractérisés par des tubes de corolle longs et les soumettre à des croisements aléatoires entre eux. Pour mettre en évidence l’efficacité de cette sélection, on propose l’étude des données expérimentales suivantes :
L’étude statistique de la distribution de la longueur du tube de la corolle dans la population mère (P1) de Longiflora, a permis l’établissement de l’histogramme de fréquence, du polygone de fréquence et le calcul des paramètres statistiques X̄ et σ. (Voir document ci-dessous)
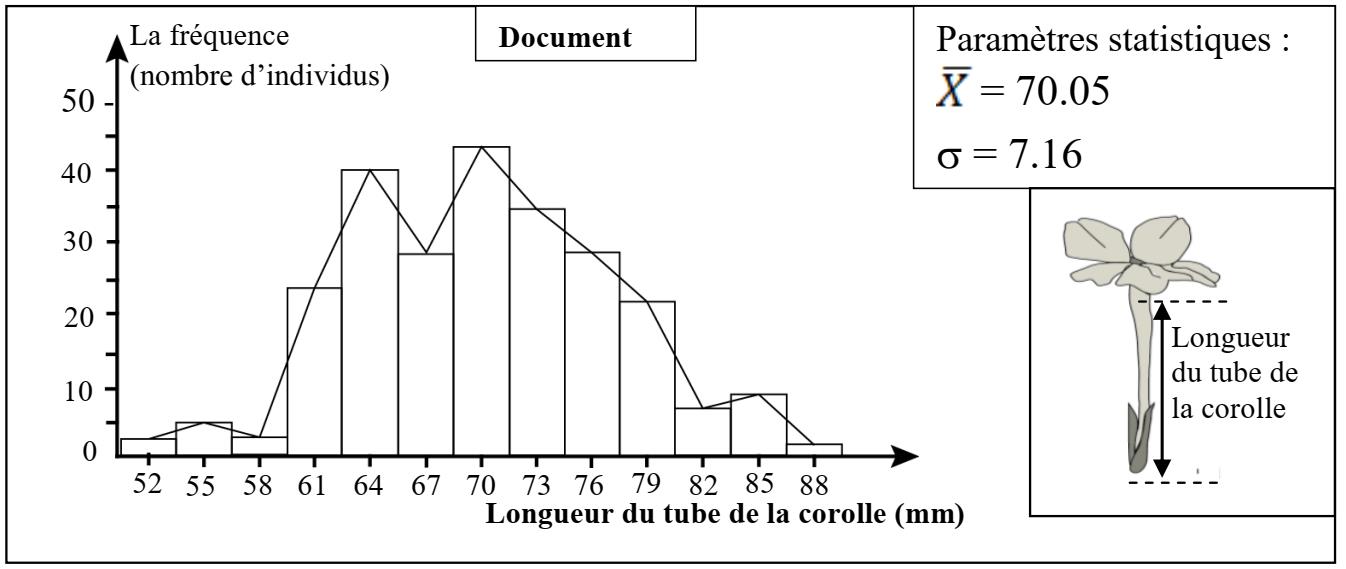
1 – En exploitant le document ci-dessus :
a – Déterminez le type de variation étudiée. (0.5 pt)
b – Décrivez la distribution de fréquence dans cette population. Qu’en déduisez-vous ? (1 pt)
Les individus caractérisés par des tubes de corolle dont la longueur est égale ou supérieure à 79 mm sont isolés et croisés entre eux au hasard. On a obtenu de ces croisements une population fille (P2). Le tableau ci-dessous représente la distribution des fréquences de la longueur du tube de la corolle chez la population P2.
La moyenne des | 52 | 55 | 58 | 61 | 64 | 67 | 70 | 73 | 76 | 79 | 82 | 85 | 88 | 91 |
Nombre | 0 | 0 | 0 | 1 | 1 | 1 | 15 | 20 | 28 | 41 | 18 | 3 | 3 | 2 |
2 – Calculer la moyenne arithmétique et l’écart-type de cette distribution. Utilisez un tableau d’application pour calculer ces paramètres. (2 pts)
On donne :
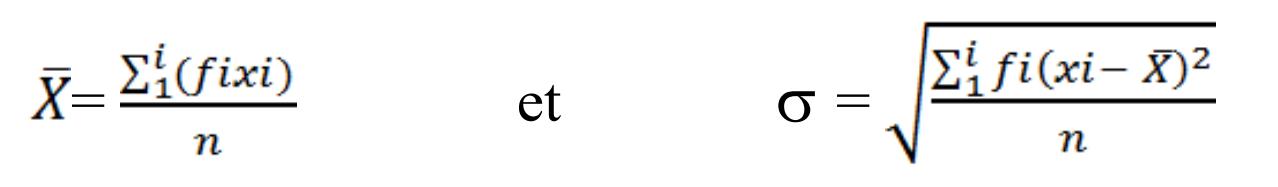
3 – Comparer les paramètres statistiques X̄ et σ des deux populations P1 et P2. Qu’en déduisez-vous à propos de l’efficacité de la sélection artificielle effectuée ? (1.5 pt)
Correction
1-a –
Il s’agit d’une variation continue (0.25pt)
Justification : la longueur du tube de la corolle peut prendre toutes les valeurs (0.25pt)
1-b –
Le polygone de fréquence montre deux modes ; le premier mode à 64 mm et le deuxième mode à 70 mm (0.5pt)
Un grand écart entre les valeurs de la longueur du tube de la corolle et la moyenne arithmétique (0.25pt)
Déduction : la population est donc hétérogène (0.25pt)
2 –
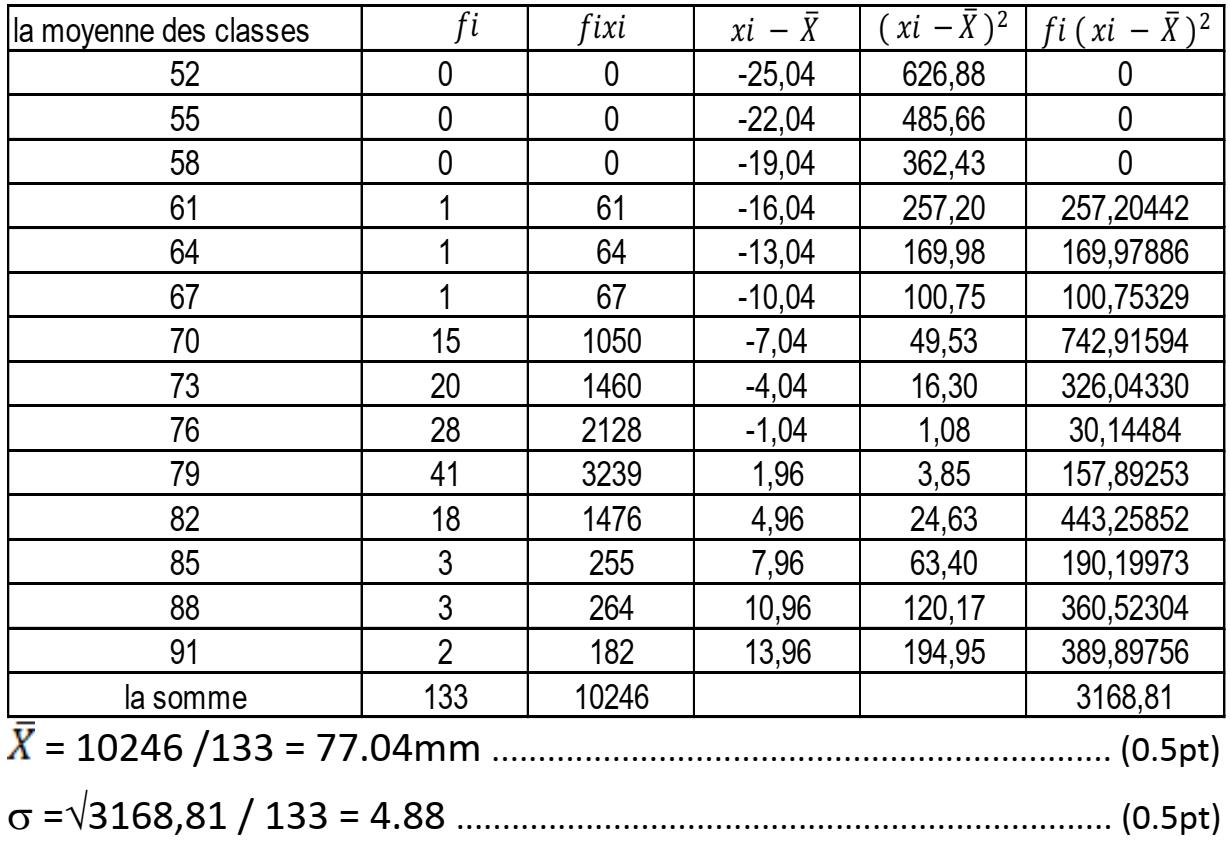
3 – La comparaison doit contenir les éléments suivants :
La moyenne arithmétique de la population fille P2 est supérieure à celle de la population mère P1 (0.5 pt)
L’écart-type de la population fille P2 est inférieur à celui de la population mère P1 (0.5 pt)
La sélection effectuée est efficace car chez la population P2 la longueur du tube de la corolle s’est améliorée et la dispersion de la population a diminué (0.5 pt)